Pistekirjoituksella tulostamista varten yhtälöt on muunnettava. Matemaattiset symbolit, kuten neliöjuuret ja monet muut, on muunnettava myös.
Matemaattiset yhtälöt ja pistekirjoitustaulukot
On välttämätöntä käyttää yhtälöiden merkintätapaa, joka on yhteneväinen pistetaulukosta riippumatta. Monet yhtälöeditorit käyttävät MathML:ää yleisenä kielenää matemaattisten yhtälöiden tallentamiseen ja käsittelyyn. Sitä käytetään myös yhtälöiden lisäämiseen TactileViewissä.
Oikean yhtälön tulostamiseksi pistekirjoituksella tarvitaan kaksivaiheinen muunnos: matemaattisten merkintäsääntöjen käyttäminen ja pistekirjoitustaulukon käyttäminen merkkien muuntamiseen yhtälöä vastaavaksi pistekirjoitukseksi.
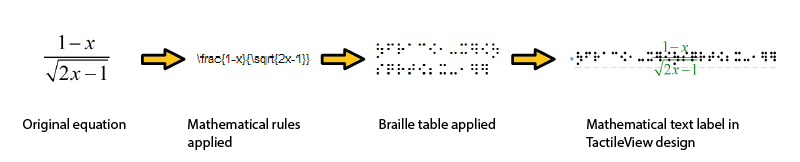
Kuva 1. Muuntaminen MathTypen yhtälöstä matemaattiseksi tekstiksi käyttämällä valittua matemaattista merkintää (tässä tapauksessa LaTeX) ja pistekirjoitustaulukkoa (en-us-comp8.ctb).
Matemaattinen merkintä käyttää sääntöjä, jotka muuntavat graafisen asettelun (MathML) koordinaattielementit tekstiriviksi. Pistemerkkejä on lisättävä, jotta voidaan osoittaa osien suhde, kuvata erityisiä matemaattisia symboleja tai merkitä elementtien loogista järjestystä. Muun muassa Nemeth, Unified Englanti pistekirjoitus, LaTeX, Marburg ja Dedicon ovat joitakin tunnetuimpia matematiikan merkitsemistyylejä ja ovat saatavilla TactileViewissä.
Ensimmäisen muuntovaiheen tuloksena yhtälö tulee luettavaksi tekstinä koordinaatiston sijaan. Toisessa vaiheessa pistekirjoituskääntäjä (TactileViewissa käytetään avoimen lähdekoodin projektia LibLouis) käyttää haluttua pistetaulukkoa muuntaakseen yhtälön tekstin pistekirjoitusmerkeiksi.
Matemaattisten kaavojen näppäimistömerkintä
Kun kirjoitat matemaattista kaavaa TactileView-näkymässä, on tärkeää käyttää oikeaa syntaksia. Matemaattisen lausekkeen elementit on syötettävä käyttämällä tiettyjen symbolien yhdistelmää ja soveltamalla tarvittaessa sulkeita. Alla olevassa luettelossa on yleiskatsaus siitä, mitä matemaattisia elementtejä tuetaan TactileView-kaavoissa. Esimerkeissä näytetään, miten näitä elementtejä käytetään ja yhdistetään.
| Matemaattinen elementti tai funktio | Symboli | Esimerkki | |
| Useiden kaavojen erottaminen toisistaan;; | y= | ||
| Kaavan parametri | x | y=x | |
| Merkit | |||
| Lisäys | + | y=x+1 | |
| Vähennyslasku | - | y=x-3 | |
| Kertolasku | * | y=2*x | |
| Jako | / | y=x/3 | |
| Eksponentti | ^ | y=2^x | |
| Sulkeet | ( ) | y= (x+2)/(x-3) | |
| Funktiot | |||
| Absoluuttinen arvo | abs( ) | y=abs(x+2) | |
| Neliöjuuri | sqrt( ) | y=sqrt(2*x) | |
| Luonnollinen logaritmi | e | ln( ) | y=ln(x-1) |
| Logaritmi ja perus 10 | log( ) | y=log(x+1) | |
| Eksponentti | jossa on e | exp( -arvo | y=exp(x^2-2*x) |
| Sini | sin( ) | sin (2 * x) | |
| Kosini | cos( ) | cos (2 * x) | |
| Tangenti | tan( ) | tan (2 * x) | |
| Arcus sini | arcus kosini tai arcus tangenti | asin( ), acos( ), atan( ) | y=asin(x-1) |
| Hyperbolinen sini | kosini tai tangentti | sinh( ), cosh( ), tanh( ) | y = sinh (x-1) |
| Hyperbolinen arcus | arcus kosini tai arcus tangenti | asinh( ),acosh( ),atanh( ) | y=asinh(x-1) |
| Vakiot | |||
| Desimaalimerkki | . | y=1 | 5*x |
| Luonnollinen logaritmipohja | e | y=e^(x^2-2*x) | |
| Pii | pi | y=sin(2*pi*x) | |
| Phi | phi | y=2*phi*x | |
| Johdannaiset | |||
| Ensimmäinen johdannainen | ' | y=(x^2-3*x+4)' | |
| Toinen johdannainen ja korkeampi | useita ' | y=(sin(2*x+1))" |

 Return to TactileView manual overview
Return to TactileView manual overview